Understanding the Tesseract, the Four-Dimensional Hypercube That Challenges Human Perception and Expands the Boundaries of Mathematics and Physics
There are shapes that we can touch, build, and see with ease, and then there are shapes that live mostly in the mind. The tesseract, also known as the hypercube, is one of those rare creations of mathematics that feels almost like a bridge to another universe. It isn’t rare because it’s hidden from us in some corner of the world, but because it exists in a dimension we cannot directly perceive. Just as a square extends into a cube when you move from two dimensions to three, the cube itself extends into a tesseract when you step into four dimensions. It is both familiar and utterly alien, a reminder of how small our perspective really is.
To imagine it, you have to think about progression. A line has two endpoints. When stretched into a square, it has four corners. Push that square into the third dimension and you get a cube with eight corners. Then, take that cube and extend it into the fourth dimension, and suddenly it becomes a tesseract with sixteen corners. Alongside those sixteen vertices come 32 edges, 24 square faces, and 8 cubic cells, all arranged not in the three-dimensional space we know but in a world of four spatial directions. It’s dizzying to think about because we’re not built to see it directly, but mathematics lays it out with perfect clarity.
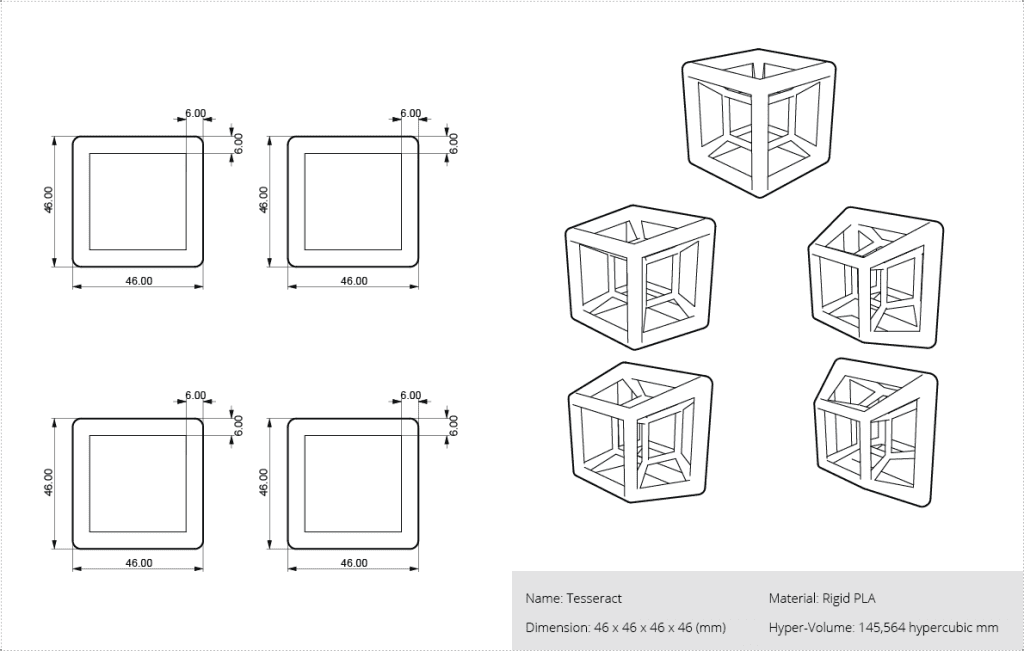
The uniqueness of the tesseract begins with its origin. Just as a cube connects two identical squares in space, the tesseract connects two identical cubes in the fourth dimension. It follows the same logic, but with an extra axis of space that we cannot point to. This makes every attempt to visualize it feel like an exercise in shadows. The classic image people know is that of a cube within a cube, connected by edges. That picture is only a projection, a 3D shadow of a 4D shape, much like a flat drawing of a cube on paper is only a 2D shadow of the real thing. What we see is never the full tesseract, only its faint imprint in the world we can understand.
Mathematically, though, it is perfectly defined. Its symmetry is expressed in the elegant Schläfli symbol {4,3,3}, a notation that encodes its balanced and repeating structure. It is one of the most important objects in higher-dimensional geometry, and for mathematicians, it serves as a cornerstone in exploring how shapes evolve when you keep adding dimensions. For physicists, it has taken on an even more symbolic role. In theories of spacetime, string theory, and cosmology, the tesseract has been used as a metaphor for dimensions beyond the three we can move in. It isn’t just a shape—it’s a concept, a hint that reality itself may be layered in ways we can’t yet grasp.

And yet, for all its beauty, the tesseract will never sit on a desk like a cube does. You can’t hold it, turn it in your hand, or build it out of wood. You can only explore it through mathematics, computer models, and imagination. That limitation is part of its strange appeal. It teases us with the possibility that the universe is much larger than the slice we experience. While we are bound to our three dimensions, the tesseract suggests that there could be more, hidden just beyond our perception, waiting for science to reveal.
For me, the tesseract is more than an abstract curiosity. It is a reminder of how far human thought can reach, even when our senses fall short. It is proof that our minds are capable of grasping truths that our eyes cannot see. Every time I look at those wireframe drawings of a cube inside a cube, I feel a mix of humility and wonder. Maybe we’ll never step into the fourth dimension, but the fact that we can describe it so clearly shows just how powerful the language of mathematics really is. The tesseract tells us that reality might hold layers we haven’t even begun to touch, and that in itself is a reason to keep exploring.


